How order emerges when matter comes alive
Physicists have long understood how order emerges in ordinary matter, like how tiny oil droplets mixed in water will coalesce until oil and water end up completely separated from each other. Whether a similar understanding of the emergence of order in living matter can be obtained, is, however, still unclear. In their new study, researchers from the Max Planck Institute for Dynamics and Self-Organization (MPIDS) in Göttingen investigated the question of how different proteins inside living cells cluster together and form liquid micro-structures, how coexisting populations of bacteria self-organize, or how groups of predators and prey interact with each other. Now, in a new paper published in Physical Review X, they have devised a ‘standard model’ to understand the result of such processes.
Interactions
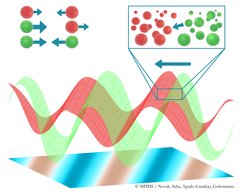
Particles of two types (red and green) interact with each other. Whereas particles of the same type necessarily experience reciprocal attraction or repulsion, particles of different types can interact non-reciprocally. Here, the green particles chase after the red particles. At large scales, high density bands of green particles chase after bands of red particles, leading to the emergence of global order and net motion in the system.
Building on earlier works on the physical characterization of phase transitions, physicists have been able to describe and predict how ‘passive’ or non-living mixtures such as oil and water aggregate or separate since the 1950s, when J.W. Cahn and J.E. Hilliard introduced the celebrated Cahn-Hilliard equation, considered the standard model of phase separation. However, a defining feature of living matter, absent in ordinary matter and thus absent in the Cahn-Hilliard equation, is non-reciprocity: for example, while oil must repel water just as much as water repels oil, a predator can be attracted to a prey while the prey tries to avoid the predator. In order to understand how large collections of ‘active’ or living entities behave, such as whether they will happily mix together or whether they will cluster into groups, these non-reciprocal interactions had to be incorporated into the formalism of phase separation. This was the key idea of the team, composed of Suropriya Saha, Jaime Agudo-Canalejo, and Ramin Golestanian, from the Department of Living Matter Physics at the Max Planck Institute for Dynamics and Self-Organization.
Many models inside one
An important feature of the Cahn-Hilliard equation is its simplicity. It captures the physics of phase separation using its most basic ingredients, with the resulting advantage that it can correctly predict features of phase separation in a wide variety of systems, no matter the specific details of the molecules involved. The Göttingen researchers say that the same applies to their non-reciprocal version of the equation. MPI Director Golestanian explains: “Active systems can be very different from each other at the single particle level, as they include everything from enzymes and motor-proteins, to man-made swimming micro-robots, bacteria, and larger scale organisms, each with their own specific features. When we describe a collection of such active systems over large distances and long periods of time, however, the specific details of the systems become less important, and ultimately the defining feature becomes the overall distribution of the systems in space. It is at this scale that our equation should capture universal features in a wide variety of active, living matter.”
Teaching an old “dog” new tricks
The team began by digging into the classical Cahn-Hilliard equation. Meant to describe non-living systems, the reciprocal nature of passive interactions is deeply embedded in the structure of the equation, which enforces thermodynamic equilibrium, in which all entities involved are ultimately at rest, as an unavoidable end-state of any process described by it. Life, on the other hand, is the most paradigmatic example of a process out of thermodynamic equilibrium. The first task of the researchers, therefore, was to find a way to break the structure of the equation, to introduce the possibility of non-reciprocal interactions and thus of processes that can describe living systems. Saha and coworkers devised a minimally-disruptive way to go about it, by introducing a single parameter describing non-reciprocal activity (in the most basic example of a two-component system) that would allow them to describe situations arbitrarily close or arbitrarily far from a passive system.
A little goes a long way
Once they had found the right way to modify the equation, the authors began to run computer simulations to evaluate the effects of activity. “Remarkably”, says Saha, first author of the study, “we found that even minimal amounts of non-reciprocity lead to radical departures from the behavior of passive systems.” Most surprisingly, the authors saw the emergence of travelling waves in which bands of one component chase after bands of the other, resulting in a pattern of moving stripes. This was unexpected because, in passive systems, particles without a sense of direction (like points or spheres) cannot self-organize into stripes. This transition, which physicists call spontaneous polar symmetry breaking, was however made possible by the non-reciprocal activity, which also broke time-reversal symmetry, a defining feature of systems out of thermodynamic equilibrium. Besides moving stripes, the group also observed that the mixtures could arrange into complex lattices where little spots of one component were chased by spots of the other. Prof. Golestanian adds: "This shows that not only does physics contribute to our understanding of biology, but also that the challenges posed by studying living matter open up new avenues for fundamental research in physics."
