Wie Ordnung entsteht, wenn Materie zum Leben erwacht
Seit langem verstehen Physiker, wie Ordnung in gewöhnlicher Materie entsteht, beispielsweise wie winzige in Wasser gemischte Öltröpfchen zusammenfließen, bis sich Öl und Wasser am Ende vollständig voneinander trennen. Ob ein ähnliches Verständnis für die Entstehung von Ordnung in lebender Materie gewonnen werden kann, ist bisher jedoch noch offen. Die Fragen, wie sich verschiedene Proteine innerhalb lebender Zellen zusammenschließen und flüssige Mikrostrukturen bilden, wie sich koexistierende Populationen von Bakterien selbst organisieren oder wie Gruppen von Rau- und Beutetieren miteinander interagieren, nahmen Forscher des Göttinger Max-Planck-Instituts für Dynamik und Selbstorganisation (MPIDS) in ihrer neuen Arbeit unter die Lupe. In der aktuell im Journal Physical Review X erschienenen Veröffentlichung konzipierten sie ein „Standardmodell“, um das Ergebnis solcher Prozesse zu verstehen.
Wechselwirkung
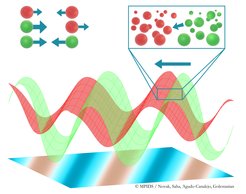
Partikel zweier Arten (rot und grün) interagieren miteinander. Während Partikel desselben Typs zwangsläufig reziproke Anziehung oder Abstoßung erfahren, können Partikel verschiedener Typen nicht reziprok interagieren. Hier jagen die grünen Partikel den roten Partikeln hinterher. In großem Umfang jagen die hochverdichten Bänder der grünen Partikel den Bändern der roten Partikel nach, was zur Entstehung einer globalen Ordnung und Bewegung im System führt.
Die Betrachtungen bauen auf früheren Arbeiten zur physikalischen Charakterisierung von Phasenübergängen auf. In den 1950er Jahren haben J.W. Cahn und J.E. Hilliard mit der berühmten Cahn-Hilliard-Gleichung das geltende Standardmodell der Phasentrennung präsentiert. Physiker können so beschreiben und vorhersagen, wie sich „passive“ oder nicht lebende Gemische wie Öl und Wasser zusammensetzen oder trennen. Ein entscheidendes Merkmal der lebenden Materie, das in der gewöhnlichen Materie und damit auch in der Cahn-Hilliard-Gleichung fehlt, ist jedoch die Nicht-Reziprozität: Während zum Beispiel Öl Wasser genauso abstoßen muss wie Wasser Öl abstößt, kann ein Raubtier von einer Beute angezogen werden, während die Beute versucht, dem Raubtier zu entkommen. Um zu verstehen, wie sich große Ansammlungen von „aktiven“ oder lebenden Einheiten verhalten, z.B. ob sie sich gerne miteinander vermischen oder zu Clustern zusammenfinden, mussten diese nicht reziproken Wechselwirkungen in den Formalismus der Phasentrennung einbezogen werden. Dies war die Grundidee des Teams, bestehend aus Suropriya Saha, Jaime Agudo-Canalejo und Ramin Golestanian von der Abteilung Physik lebender Materie am Max-Planck-Institut für Dynamik und Selbstorganisation.
Viele Modelle in einem
Ein wichtiges Merkmal der Cahn-Hilliard-Gleichung ist ihre Einfachheit. Sie erfasst die Physik der Phasentrennung unter Verwendung ihrer grundlegendsten Bestandteile, mit dem daraus resultierenden Vorteil, dass die Merkmale der Phasentrennung in zahlreichen Systemen korrekt vorhegesagt werden können, unabhängig von den spezifischen Eigenschaften der beteiligten Moleküle. Nach Ansicht der Göttinger Forscher gilt dasselbe für ihre nicht-reziproke Version der Gleichung. MPI-Direktor Golestanian erklärt: „Aktive Systeme können auf der Ebene einzelner Partikel sehr heterogen sein, da sie alle möglichen Einheiten, von Enzymen und Motorproteinen bis hin zu künstlich erstellten schwimmenden Mikrorobotern, Bakterien und größeren Organismen beinhalten, wobei jedes System eigene spezifische Eigenschaften aufweist. Wenn wir eine Gruppe solcher aktiven Systeme über große Entfernungen und lange Zeiträume beschreiben, verlieren die spezifischen Details der Systeme jedoch an Bedeutung, und letztlich wird deren Gesamtverteilung im Raum zum entscheidenden Merkmal. Genau in diesem Rahmen sollte unsere Gleichung universelle Merkmale in einer Vielzahl von aktiver, lebender Materie erfassen.“
Einem alten „Hund“ neue Tricks beibringen
Das Forscherteam begann damit, die klassische Cahn-Hilliard-Gleichung unter die Lupe zu nehmen. Da die Gleichung nicht-lebende Systeme beschreibt, ist die Reziprozität passiver Interaktionen tief in deren Struktur eingebettet. Das thermodynamische Gleichgewicht, in dem sich schließlich alle Akteure in einem Ruhezustand befinden, ist stets der Endzustand jedes von ihr beschriebenen Prozesses. Das Leben hingegen ist das Paradebeispiel für einen Prozess außerhalb des thermodynamischen Gleichgewichts. Die erste Aufgabe der Forscher bestand daher darin, einen Weg zu finden, die Struktur der Gleichung so zu brechen, dass sie nicht-reziproke Wechselwirkungen einbezieht und somit auch entsprechende Prozesse, um nun die lebenden Systeme beschreiben zu können. Saha und ihre Kollegen erarbeiteten einen minimal-invasiven Ansatz, indem sie einen einzigen Parameter einführten, der nicht-reziproke Aktivitäten charakterisiert (am einfachsten Beispiel eines Zweikomponentensystems). Dies würde ermöglichen, Situationen zu beschreiben, die sich einem passiven System beliebig ähneln oder davon beliebig unterscheiden.
Wenig kann sehr viel bewirken
Nachdem sie den richtigen Weg gefunden hatten, die Gleichung zu modifizieren, haben die Autoren Computersimulationen durchgeführt, um die Auswirkungen der Aktivität zu bewerten. „Erstaunlicherweise“, so Saha, die Erstautorin der Studie, „stellten wir fest, dass selbst eine minimale Nicht-Reziprozität zu radikalen Abweichungen vom Verhalten passiver Systeme führt“. Überraschenderweise beobachteten die Autoren die Entstehung von Wanderwellen, bei denen Bänder der einen Komponente den Bändern der anderen nachjagten, was zu einem Muster von sich bewegenden Streifen führte. Dies war unerwartet, weil sich in passiven Systemen Partikel ohne Orientierungssinn (wie Punkte oder Kugeln) nicht selbst zu Streifen organisieren können. Dieser Übergang, den Physiker als eine spontane polare Symmetriebrechung bezeichnen, wurde jedoch durch die nicht-reziproke Aktivität ermöglicht, die auch die zeitumkehrende Symmetrie brach, ein entscheidendes Merkmal von Systemen außerhalb des thermodynamischen Gleichgewichts. Außerdem haben die Forscher beobachtet, dass die Gemische komplexe Gitter bilden konnten, in denen kleine Spots der einen Komponente durch Spots der anderen Komponente gejagt wurden. „Dies zeigt“, ergänzt Prof. Golestanian, „dass die Physik nicht nur zu unserem Verständnis der Biologie beiträgt, sondern auch, dass die Herausforderungen des Erforschens lebender Materie neue Wege für die physikalische Grundlagenforschung eröffnen“.
