Topologie in der Biologie
Ein aus Quantensystemen bekanntes Phänomen wurde nun auch im Zusammenhang mit biologischen Systemen beschrieben: In einer neuen Studie, die in Physical Review X veröffentlicht wurde, zeigen Forscher des Max-Planck-Instituts für Dynamik und Selbstorganisation (MPI-DS) in Göttingen, dass der Begriff des topologischen Schutzes auch für biochemische Netzwerke gelten kann. Da diese typischerweise sehr komplex sind und dennoch sehr stabil gegenüber Veränderungen bleiben, kann die Topologie bei der Entstehung von robusten Schwingungen helfen. Das von den Wissenschaftlern entwickelte Modell macht den topologischen Werkzeugkasten, der typischerweise nur zur Beschreibung von Quantensystemen verwendet wird, nun auch für die Biologie verfügbar.
Wann kann man sagen, dass eine bestimmte Eigenschaft eines Systems robust ist? Intuitiv bedeutet Robustheit, dass die besagte Eigenschaft auch unter der Einwirkung von externen Störungen auf das System, egal wie stark oder zufällig, unverändert bleibt. In der Mathematik werden Eigenschaften eines Objekts, die robust gegenüber Verformungen sind, als topologisch bezeichnet. Zum Beispiel können die Buchstaben s, S und L ineinander umgewandelt werden, indem man ihre Form dehnt oder krümmt. Das Gleiche gilt für die Buchstaben o, O und D. Es ist jedoch unmöglich, ein S in ein O zu verwandeln, ohne eine diskontinuierliche Operation durchzuführen, wie z. B. das Zerschneiden des O oder das Zusammenkleben der beiden Enden des S. Daher sagen wir, dass die Buchstaben s, S und L die gleiche Topologie haben - ebenso wie die Buchstaben o, O und D - während die beiden Buchstabengruppen unterschiedliche Topologien haben. Aber was hat die Topologie mit der Biologie zu tun?
"In den letzten Jahrzehnten haben Physiker herausgefunden, dass bestimmte Eigenschaften von Quantensystemen nur von der Topologie eines zugrunde liegenden Merkmals des Systems abhängen, wie z. B. die Phase seiner Wellenfunktion oder sein Energiespektrum", erklärt Evelyn Tang, Co-Erstautorin der Studie. "Wir wollten wissen, ob sich dieses Modell auch auf biochemische Systeme anwenden lässt, um Prozesse außerhalb des Gleichgewichts besser beschreiben und verstehen zu können." Da die Topologie unempfindlich gegenüber kontinuierlichen Störungen ist - wie das Dehnen oder Biegen von Buchstaben im obigen Beispiel - sind die mit der Topologie verbundenen Eigenschaften extrem robust. Sie bleiben unverändert, es sei denn, es kommt zu einer qualitativen Veränderung des Systems, wie z. B. dem Auseinanderschneiden oder Zusammenkleben der obigen Buchstaben. Die Wissenschaftler Evelyn Tang, Jaime Agudo-Canalejo und Ramin Golestanian haben nun gezeigt, dass das gleiche Konzept des topologischen Schutzes auch in biochemischen Systemen zu finden ist, was die Robustheit der entsprechenden biochemischen Prozesse gewährleistet.
Fluss entlang der Kanten
|
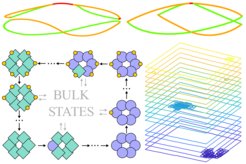
Oben: Wie ein S, das sich in ein O verwandelt, kann das Spektrum eines biochemischen Systems einen topologischen Übergang erfahren. |
Eine der bekanntesten Beobachtungen zur Topologie in Quantensystemen ist der Quanten-Hall-Effekt: Dieses Phänomen tritt auf, wenn ein zweidimensionales leitendes Material einem senkrechten Magnetfeld ausgesetzt wird. In einer solchen Umgebung beginnen die Elektronen im Material, sich in winzigen Kreisen, den sogenannten Zyklotronbahnen, zu bewegen, die insgesamt zu keinem Nettostrom in der Masse des Materials führen. An den Rändern des Materials werden die Elektronen jedoch abprallen, bevor sie eine Umlaufbahn vollenden, und sich effektiv in die entgegengesetzte Richtung bewegen, was zu einem Nettostrom von Elektronen entlang dieser Ränder führt. Wichtig ist, dass dieser Kantenfluss unabhängig von der Form der Kanten auftritt und auch dann bestehen bleibt, wenn die Kanten stark verformt werden, was die topologische und damit robuste Natur des Effekts unterstreicht.
Den Forschern fiel eine Parallele zwischen solchen Zyklotronbahnen im Quanten-Hall-Effekt und einer Beobachtung in biochemischen Systemen auf, die als "nutzlose Zyklen" bezeichnet werden: Gerichtete Reaktionszyklen, die zwar Energie verbrauchen, aber zumindest auf den ersten Blick nutzlos sind. Zum Beispiel kann eine Chemikalie A in B umgewandelt werden, die wiederum in C umgewandelt wird, welche anschließend in A umgewandelt wird. Dies warf die Frage auf: Ist es möglich, dass analog zu den Zyklotronbahnen im Quanten-Hall-Effekt, vermeintlich nutzlose Zyklen Kantenströme verursachen können, die dann zu einem Nettofluss in einem zweidimensionalen biochemischen Reaktionsnetzwerk führen?
Die Autoren modellierten daher biochemische Prozesse, die in einem zweidimensionalen Raum ablaufen. Ein einfaches Beispiel ist die Montagedynamik eines Biopolymers, das aus zwei verschiedenen Untereinheiten X und Y zusammengesetzt ist: Ein nutzloser Zyklus im Uhrzeigersinn würde dann dem Hinzufügen einer Y-Untereinheit, dem Hinzufügen einer X-Untereinheit, dem Entfernen einer Y-Untereinheit und dem Entfernen einer X-Untereinheit entsprechen, was das System wieder in den Ausgangszustand bringt. In einem solchen zweidimensionalen Raum existieren jedoch auch "Kanten", welche Einschränkungen in der Verfügbarkeit von Untereinheiten darstellen. Wie erwartet, fanden die Forscher heraus, dass entlang dieser Kanten tatsächlich spontan gegenläufige Ströme entstehen. Jaime Agudo-Canalejo, Co-Erstautor der Studie, erklärt: "In diesem biochemischen Kontext entsprechen die Kantenströme großräumigen zyklischen Oszillationen im System. Im Beispiel eines Biopolymers würden sie zu einem Zyklus führen, bei dem zuerst alle X-Untereinheiten im System dem Polymer hinzugefügt werden, gefolgt von allen Y-Untereinheiten, dann werden zuerst alle X- und schließlich alle Y-Untereinheiten wieder entfernt, so dass der Zyklus abgeschlossen ist."
Die Bedeutung von Topologie
Ähnlich wie im Quanten-Hall-System scheinen solche biochemischen Kantenströme robust gegenüber Veränderungen der Form der Systemgrenzen oder gegenüber Unordnung in der Masse des Systems zu sein. Die Wissenschaftler wollten daher herausfinden, ob die Topologie tatsächlich der Grund für diese Robustheit ist. Die in Quantensystemen verwendeten Werkzeuge sind jedoch nicht direkt auf biochemische Systeme anwendbar, da diese den klassischen stochastischen Gesetzen unterliegen. Zu diesem Zweck entwickelten die Forscher ein Mapping zwischen ihrem biochemischen System und einer exotischen Klasse von Systemen, die als nicht-hermitsche Quantensysteme bekannt sind. Evelyn Tang, die einen Hintergrund in topologischer Quantenmaterie hat, erinnert sich: "Sobald diese Abbildung etabliert war, stand uns der gesamte Werkzeugkasten der topologischen Quantensysteme zur Verfügung. Wir konnten daraufhin zeigen, dass die Kantenströme dank des topologischen Schutzes tatsächlich robust sind. Außerdem fanden wir heraus, dass das Auftreten von Kantenströmen untrennbar mit der Ungleichgewichtsnatur der nutzlosen Zyklen verbunden ist, die durch den Energieverbrauch angetrieben werden."
Ein neues Reich der Möglichkeiten
Die Robustheit, die sich aus dem topologischen Schutz ergibt, gepaart mit der Vielseitigkeit, die biochemischen Netzwerken innewohnt, führt zu einer Vielzahl von Phänomenen, die in diesen Systemen beobachtet werden können. Beispiele dafür sind eine entstehende molekulare Uhr, die einige Eigenschaften von periodischen Systemen reproduzieren kann, dynamisches Wachstum und Schrumpfen von Mikrotubuli (Proteine des Zellskeletts) sowie die spontane Synchronisation zwischen zwei oder mehr Systemen, die durch einen gemeinsamen Pool von Ressourcen gekoppelt sind. Ramin Golestanian, Co-Autor der Studie und Direktor der Abteilung für Physik lebender Materie am MPI-DS, blickt optimistisch in die Zukunft: "Unsere Studie schlägt zum ersten Mal minimale biochemische Systeme vor, in denen topologisch geschützte Kantenströme entstehen können. Angesichts der Fülle an biochemischen Netzwerken, die in der Biologie existieren, glauben wir, dass es nur eine Frage der Zeit ist, bis Beispiele gefunden werden, in denen topologischer Schutz die Vorgänge in solchen Systemen empfindlich kontrolliert."
