Streifen, Punkte, Wellen
Forscher des Göttinger Max-Planck-Instituts für Dynamik und Selbstorganisation bringen Turings Muster an neue Grenzen
Die Natur fasziniert uns mit ihren auffälligen Mustern, den Streifen oder Punkten auf Tierfellen oder Muscheln. Wie diese Muster entstehen, beschäftigt Wissenschaftler seit vielen Jahrzehnten, seit der Pionierarbeit von Alan Turing, dem bekannten britischen Mathematiker des vergangenen Jahrhunderts. In der aktuellen Ausgabe von Proceedings of the National Academy of Science (PNAS) zeigen Jean-Daniel Julien und Karen Alim der Forschergruppe „Biologische Physik und Morphogenese“ vom Max-Planck-Institut für Dynamik und Selbstorganisation (MPIDS), wie Strömungen die an Musterbildungsprozesse koppeln, die üblichen Grenzen der Mustergröße durchbrechen können. Hier reicht alleine, dass Strömungen einen der Botenstoffe des Musterbildungsprozesses mit sich reißen. Der neu entdeckte Mechanismus ermöglicht es daher, die üblichen Einschränkungen der Mustergröße, die durch physikalische Parameter begrenzt wird, zu überwinden. In Zukunft könnte dieser neu entdeckte Mechanismus der Strömungen genutzt werden, um Flüssigkeiten oder starre Objekte über lange Strecken in intelligenten Materialien, zum Beispiel aktiven Hydrogelen zu bewegen.
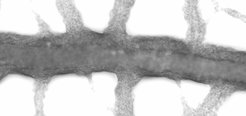
Physarum polycephalum, eines der Modellobjekte der Forschungsgruppe Biologische Physik und Morphogenese, ist bekannt für seine langreichweitigen Strömungen, die durch die bemerkenswert organisierten wellenförmigen Kontraktionen seiner netzwerkartigen Röhren erzeugt werden.
Flüsse über bemerkenswert lange Strecken sind entscheidend für das Funktionieren vieler Organismen in allen Lebensbereichen. Sie sind von grundlegender Bedeutung, um die für Migration oder Entwicklung erforderlichen Deformationen zu erzeugen oder Ressourcen und Signale zu verteilen. Einer der Hauptmechanismen, um solche Ströme zu erzeugen, sind sich ausbreitende wellenförmige Muster aus zusammengezogenen und gedehnten Bereichen. Je länger sich die Wellenlänge des Musters verzweigt desto stärker sind die Ströme. Wie Alan Turing bereits bemerkte, ist die Mustergröße jedoch durch die physikalischen Parameter begrenzt. Können wir diese Grenze überschreiten, indem die Ströme an die Bewegung des Zusammenziehens und anschließenden Dehnens gekoppelt werden?
Das Eine bedingt das Andere
Die Forscher untersuchten nun in einem mathematischen Modell die möglichen Auswirkungen von Strömungen auf Muster. Ein Signalmolekül aktiviert die Wellenmuster, wird aber auch mit dem von ihm erzeugten Fluss selbst transportiert. Der Transport erleichtert die Ausbreitung der Moleküle, was wiederum die Organisation verbessert und die Grenze der Größe des Wellenmusters um fast eine Größenordnung verschiebt. Dieser einfache Mechanismus erklärt das Entstehen von weitreichenden Mustern, deren Größen die physischen Einschränkungen durchbrechen.
"Unsere Arbeit zeigt die Bedeutung aktiver Ströme in biophysikalischen Mustermodellen, nicht nur als regulierender Input oder in sich schlüssigem Output, sondern auch als kompletter Teil einer selbstorganisierten Maschinerie", sagt Physiker Julien. "Kontraktionen und Flüssigkeitsströmungen werden in allen Arten von Organismen beobachtet, so dass unser neues Konzept wahrscheinlich für eine breite Klasse von Systemen relevant sein wird, insbesondere bei der Entwicklung von Organismen, wo Signalmoleküle in kurzer Zeit recht große Distanzen überbrücken müssen.“, unterstreicht Dr. Karen Alim als Leiterin der Forschungsgruppe „Biologische Physik und Morphogenese“ am MPIDS.
