Motile active matter
We use the framework of nonequilibrium statistical mechanics to characterize the self-organized behavior of active systems.
Living matter sustains itself out of equilibrium by constantly transforming the energy present in its surroundings to produce forces or generate motion. Without the constraints set by the Boltzmann statistics, such activity leads to emergent properties that most often defy our intuition based on equilibrium physics. Using nonequilibrium statistical mechanics tools, we design and study minimal models with the aim of uncovering the basic physical principles at play in active systems.
Image credits: Viktoria Novak
Bose-Einstein-like condensation in active matter A striking property of active systems is their ability of clusterize even in absence of attractive interactions between their individual constituents. Activity, and in particular motility, therefore constitutes a generic route to self-organization. Active systems may moreover exhibit properties analogous to that predicted by quantum mechanics. An example of such `quantum-like’ emergent behavior studied in our group occurs in nonequilibrium systems whose mean field density dynamics obeys a Fokker-Planck-type equation presenting a diffusivity edge. Despite these systems being classical, when confined in a finite volume by an external potential their diffusivity edge generically leads them to condensate at the point with lowest energy in a Bose-Einstein-like fashion. While initially predicted from a theoretical mean field description, we have recently shown that such Bose-Einstein-like condensation occurs in an experimentally relevant model of magnetic micro-swimmers.
Emergent order in active systems Active systems, as passive ones, may exhibit orientational order, the most striking example being certainly the polar order found in flocks. Nematic order is also relevant to living matter as it is involved in various biological systems including microtubule suspensions, bacterial colonies and eukaryotic cell monolayers. In both passive an active matters, topological defects moreover play a prominent role in the dynamics of order. Using a combination of microscopic models and field theories, we study various aspects of ordered active suspensions such as the transition to collective motion, the characterisation of long-range order, as well as the nonequilibrium dynamics of defects.
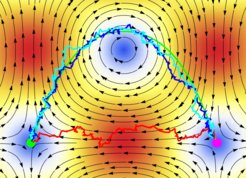
Optimal navigation in complex environment Optimal navigation, i.e. finding the fastest path connecting two points in the presence of a force landscape affecting the particle motion, has obvious practical applications. In the presence of stochasticity so that the particle trajectory generally deviates from the predetermined optimal route, optimal navigation protocols usually suppose a full control of the motion at all times, which is not always possible. We design new strategies for optimal navigation of active swimmers in complex noisy environments. Contrary to most strategies based on optimal control theory, the protocols we propose allow for semi-autonomous navigation as they do not require global knowledge of the environment, neither an external control of the particle’s motion.
Recent publications
Benoît Mahault, Evelyn Tang, Ramin Golestanian, A Topological Fluctuation Theorem, Nature Communications 13, 3036 (2022).
Benoît Mahault, Prakhar Godara, Ramin Golestanian, Emergent Organization and Polarization due to Active Fluctuations, arXiv preprint arXiv.2203.12973 (2022).
Lorenzo Piro, Benoît Mahault, Ramin Golestanian, Optimal navigation of microswimmers in complex and noisy environments New J. Phys. 24 093037 (2022).
Fanlong Meng, Daiki Matsunaga, Benoît Mahault, and Ramin Golestanian, Magnetic microswimmers exhibit Bose-Einstein-like condensation, Phys. Rev. Lett. 126, 078001 (2021).
Benoît Mahault, and Ramin Golestanian, Bose–Einstein-like condensation due to diffusivity edge under periodic confinement, New J. Phys. 22 063045 (2020).