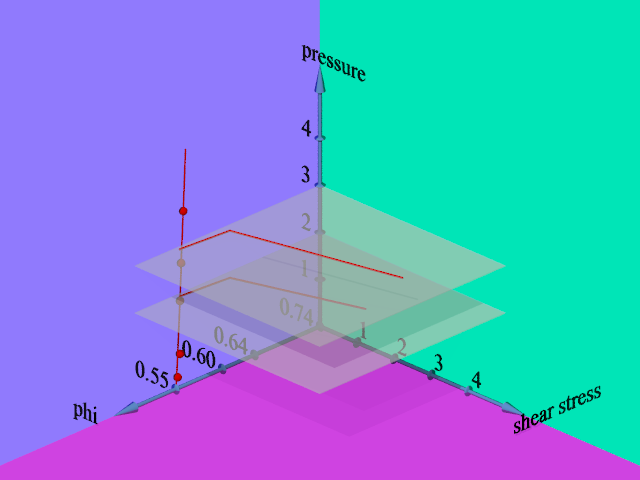
Dynamics of Complex Fluids
A complex fluid consists of (a large number of) similar mobile entities which are complex enough by themselves to preclude a straightforward prediction of the collective behaviour of the whole. Our research aims at understanding phenomena of self-organization, such as pattern formation and self-assembly, in complex fluids. We hope to identify suitable model systems which yield insight into overarching principles of self-organization in systems as diverse as aggregation of planetesimals in primordial clouds, swarming in bacterial colonies, or patterns in traffic flow. One challenging question is: are there general common ‘principles’ behind the various instances of symmetry breaking, structure formation, and emergence in open systems? Either finding such principles or proving their non-existence would be equally rewarding.
On the fundamental side, we consider general descriptions of systems far from equilibrium, such as Master equations and the Fokker-Planck equation. It is known that when a system is classified not according to its macrostates, but according to closed cycles in the space of macrostates, the corresponding Master equation retains detailed balance. We explore the possibilities to exploit this fact in the continuum (Fokker-Planck) picture, trying to find analytical expressions for the relative weights of non-equilibrium steady states.
On the complex side, biological matter provides the most intricate systems we are studying, but we try to concentrate on those which are still simple enough to be described by physical and physico-chemical principles. The swarming behaviour of Chlamydomonas reinhardtii compares well with observations in active emulsions, although there are bio-specific ramifications which are by no means understood.
The project with by far the closest connection to everyday life concerns collective behaviour in public transportation systems. After having studied the mean-field behaviour of ride pooling systems analytically and by simulations, we are performing real-world experiments (pilot projects) in order to test and develop a demand-driven system which may become comfortable and cheap enough eventually outcompete the private car on our roads.
On the fundamental side, we consider general descriptions of systems far from equilibrium, such as Master equations and the Fokker-Planck equation. It is known that when a system is classified not according to its macrostates, but according to closed cycles in the space of macrostates, the corresponding Master equation retains detailed balance. We explore the possibilities to exploit this fact in the continuum (Fokker-Planck) picture, trying to find analytical expressions for the relative weights of non-equilibrium steady states.
On the complex side, biological matter provides the most intricate systems we are studying, but we try to concentrate on those which are still simple enough to be described by physical and physico-chemical principles. The swarming behaviour of Chlamydomonas reinhardtii compares well with observations in active emulsions, although there are bio-specific ramifications which are by no means understood.
The project with by far the closest connection to everyday life concerns collective behaviour in public transportation systems. After having studied the mean-field behaviour of ride pooling systems analytically and by simulations, we are performing real-world experiments (pilot projects) in order to test and develop a demand-driven system which may become comfortable and cheap enough eventually outcompete the private car on our roads.