
Experimental Statistical Physics
Group funded by the Heisenberg program of the Deutsche Forschungsgemeinschaft
Two dimensional colloidal systems

I am interested in structure formation, self organization, spontaneous symmetry breaking (in and out of equilibrium), and dynamic arrest with focus on the underlying microscopic processes. The physics of low dimensional systems is often more complex and possesses a richer variety of excited states compared to 3D systems. Examples range from Quantum Hall effect for 2D electron ensembles in MOSFET or Dirac cones in Graphene to classical systems and their phase transitions in 2D. For long, only a few analytic theories to calculate phase transitions existed in 3D, e.g. the spherical model [Phys. Rev.: 86, 821 (1952)] but renormalization group theory became a powerful tool [Phys. Rep.: 368, 549 (2002)]. In two dimensions, a detailed theory based on the renormalization group was developed in the '70s, describing melting by topological defects. The so-called Kosterlitz-Thouless-Halperin-Nelson-Young theory (in short KTHNY theory) [J. Phys. C: 5, L124 (1972)] , [J. Phys. C: 6, 1181 (1973)], [Phys. Rev. Lett: 41, 121 (1978)], [Phys. Rev. B: 19, 2457 (1979)], [Phys. Rev. B: 19, 1855 (1979)], became prominent to a broad audience: in 2016 Michael Kosterlitz and David Thouless were awarded with the Nobel-Prize for their contributions to this 2D melting theory.
Using a colloidal ensemble (a monolayer of mesoscopic particles undergoing Brownian motion) we were successful to proof KTHNY theory in all aspects. In his Nobel Lecture, Mike Kosterlitz highlighted our experimental work about topological phase transitions in colloidal monolayers [Rev. Mod. Phys.: 89, 040501 (2017)] : "One of the main measurable predictions of the dislocation theory of melting is the renormalized (measured) Young’s modulus for which there is remarkable agreement between experiment and theory as shown in Fig. 5. Although the theoretical predictions were made in the 1970s (Halperin and Nelson, 1978, 1979; Young, 1979), experimental measurements (Zanghellini, Keim, and von Grünberg, 2005; von Grünberg, Keim, and Maret, 2007) were not done for several decades because of the difficulties of realizing a suitable experimental system." (see also [https://www.nobelprize.org/uploads/2018/06/kosterlitz-lecture.pdf] - Fig. 5 in the Nobel-talk got the copyright from [Jour. Phys. Cond. Matt.: 17, S3579 (2005)] : the "suitable experimental system" mentioned by Michael Kosterlitz is the extremely well equilibrated and characterized colloidal monolayer investigated in my group.
Symmetry breaking in equilibrium: melting in 2D and KTHNY theory

Dating back to the 1930s it was discussed (among others) by Felix Bloch, Rudolf Peierls and Lew Landau if crystals (or long range magnetism) can exist at all in low dimensions [Zeitschrift für Physik: 61, 206 (1930)] [Helv. Phys. Acta: 7, 81 (1934)] [Phys. Z. Sowj.: 11, 545 (1937)]. A rigid calculation about the lack of globally broken translational symmetry in two dimensions is given in the Mermin-Wagner-Hohenberg theorem . For 2D crystals, it claims that the displacement of lattice sites grows logarithmically with system size [Phys. Rev. Lett.: 17, 1133 (1966)] [Phys. Rev.: 176, 250 (1968)] [Phys. Rev.: 158, 383 (1937)] . Interestingly, this logarithmic divergence has not yet been measured in 2D crystals - neither in colloidal monolayers, nor in graphene. The logarithmic divergence implies that spontaneous symmetry breaking cannot exist in 2D. This prediction was often misinterpreted and let to the assumption that 2D crystals cannot exist. Indeed, it was exactly the discrepancy between this interpretation of the Mermin-Wagner-Hohenberg theorem and the results of the first computer simulations by Alder and Wainwright (indicating crystallization in two dimensions) [Phys. Rev.: 127, 359 (1962)] , which once motivated Michael Kosterlitz to work as postdoc in David Thouless' group about topological phase transitions [Jour. Phys. Cond. Matt.: 28, 481001 (2016)]. Kosterlitz and Thouless predicted a continuous transition induced by topological defects (dislocations), while other theories and the computer simulations suggested a single first order transition [Phys. Rev. Lett.: 48, 933 (1982)]. In the following, the mechanism of 2D melting has been a matter of debate over decades.
Based on the work of Kosterlitz and Thouless, David Nelson and Bertrand Halperin foretold the existence of a hexatic phase as an intermediate phase between the isotropic liquid and crystal. 2D systems should undergo two continuous transitions, mediated by two different types of thermally activated topological defects (dislocations and disclinations) - the orientational and translational symmetries are broken at different temperatures. The intermediate hexatic phase is a kind of liquid crystal in 2D with six-folded director field and has been verified in such 2D colloidal systems [Phys. Rev. Lett.: 58, 1200 (1987)] [Phys. Rev. Lett.: 73, 3113 (1994)] [Phys. Rev. Lett.: 82, 2721 (1999)]. Indeed the transitions were identified to be continuous if the system is always kept in thermal equilibrium. Our results support the two-step-melting and KTHNY theory in all aspects and the critical exponents fit very well to the results of renormalization group theory [Phys. Rev. E: 75, 031402 (2007)] [Chem. Phys. Chem.: 11, 963 (2010)]. Supported by simulations we were even able to measure the specific heat of the colloidal ensemble: in the crystal, we recovered Dulong Petit's law; for the transition points, we showed that the specific heat is given by the unbinding of topological defects [Phys. Rev. Lett.: 113, 127801 (2014)] and the associated discrete core energy of dislocations and disclinations, respectively [Phys. Rev. Lett.: 95, 185502 (2005)].
Symmetry breaking far from equilibrium; Kibble-Zureck-mechanism
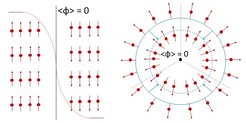
Standard thermodynamics fails to describe macroscopic observables in systems far from equilibrium. Unlike during melting in 2D, we do not observe a hexatic phase in experiments during freezing, cooling the system from the high to the low symmetry phase. This contradicts the assumption that phase transitions should be reversible if they mediate between well defined thermodynamic states. Quenching the system, we observe poly-crystalline solids. The framework is given within the so-called Kibble-Zurek mechanism, which describes the evolution of topological defect structures like domain walls, strings, and monopoles when a system is driven at a finite cooling rate through a second order phase transition. The model was originally developed by Tom Kibble for the primordial Higgs field shortly after Big Bang (meanwhile frequently called Inflaton) [Jour. Phys. A: 9, 1387 (1976)] [Phys. Rep.: 67, 183 (1980)]. Wojciech Zurek applied it on a very different scale to quantum fluids and liquid crystals in condensed matter systems [Nature: 317, 505 (1985)] [Phys. Rep.: 276, 177 (1996)]. The observed defect structure naturally arises during cooling if spatially separated regions are disconnected by causality: regions which are separated by such distances that they cannot "communicate" about their local symmetry (at the given age of the university) cannot gain the same value of the order-parameter during spontaneous symmetry breaking. In cosmology, this finite signal velocity is ultimately given by the speed of light times the expansion rate of the universe. This limited signal velocity defines a cosmic event horizon at the given age of the universe. In condensed matter systems, signals are limited by the sound velocity (or second sound in suprafluid Helium) defining a "sonic horizon". Cooling at finite rates results in separated domains with different degenerated values of the order parameter. We showed that typical length scales of the defect network in our colloidal monolayer varies as function of cooling rate as precisely described by the Kibble-Zurek mechanism when adopted for the Kosterlitz-Thouless universality [Proc. Natl. Acad. Sci.: 112, 6925 (2015)]. Thus the colloidal monolayer shows fascinating similarities with quantum fluids and even the primordial Higgs-field in Big-Bang theories. The analogies between the very different ensembles arise by the two component (or complex) order parameter which they have in common. This work is highlited [Proc. Natl. Acad. Sci.: 112, 6780 (2015)] in PNAS and awarded with the Gustav-Hertz prize of the German Physical Society.
Amorphous systems and vitrification

Other systems being out of equilibrium are glasses. "Technology" of mankind started in the Stone Age more than a million years ago by the use of glassy materials (e.g. obsidian) to construct the first primitive tools like the biface. Yet, there is still no theoretical description of glassy materials able to explain all phenomena observed during vitrification. From a technological point of view, a supercooled fluid is called a glass, if the viscosity exceeds 1012 Pa·s irrespective of whether it stays finite or diverges at an ideal glass transition [Nature: 410, 259 (2001)]. For fast cooling rates this threshold is reached at a higher temperature, while for slow cooling at a lower one. The transition temperature TG depends on history and thus the glass transition does not mediate between well defined thermodynamic states. While Mode-Coupling theory (MCT) can explain the dynamic bifurcation as function of temperature by solving integro-differential equations of correlated density fluctuations, other theories as e.g. Random First Order Transition (RFOT) theories explain the glass transition by an underlying phase transition which is not reached due to diverging viscosities. Diverging viscosities imply diverging relaxation times. But diverging timescales are problematic to be proven in simulation or experiment. While viscosity refers to liquids, shear elasticity contains complementary information from the solid state side. To avoid diverging relaxation times, my group thus experimentally investigated the elastic properties of a colloidal glass former near the glass transition: we showed that the shear elasticity disappears discontinuously. For the given cooling rate, this determines the transition temperature unambiguously and directly addresses questions about elasticity during vitrification [Phys. Rev. X: 5, 041033 (2015)], namely the continuous [Phys. Rev. Lett: 105, 015504 (2010)] versus discontinuous behaviour of elasticity [Phys. Rev. Lett.: 107, 105505 (2011)] [Phys. Rev. Lett: 109, 178301 (2012)].
Long wavelength instabilities: Goldstone-modes and Mermin-Wagner-theorem
It is now well established, that crystallization differs significantly in two and three dimensions. Whether the glass transition is dimensional dependent is an open question, beside theories predicting an ideal glass transition in infinite dimensions [Jour. Stat. Mech.: 2012, P10012 (2012)]. In 2015 results from extensive computer simulations of the glass transition in 2D and 3D ensembles were reported. It was found that the transient behaviour in 2D is significantly less pronounced compared to 3D. Furthermore a decoupling of orientational and translational degrees of freedom in 2D was reported which was not present in 3D [Nat Comm.: 6, 7392 (2015)]. It is been concluded, that the glass transition scenarios differ in 2D and 3D. We showed, that the differences found in the simulations can be explained with long wavelength fluctuations of Mermin-Wagner-Hohenberg type originally explaining the lack of symmetry breaking in 2D crystals. This works without necessarily changing the microscopic picture between the 2D and 3D glass transition. Comparing data from 2D colloidal crystals, 2D colloidal glasses, 3D colloidal glasses, and 2D computer simulations. The existence of Mermin-Wagner-Hohenberg fluctuations in amorphous 2D solids was clearly demonstrated. The computer simulations were even able to proof the 'smoking gun' of Mermin-Wagner fluctuations, namely the logarithmic divergence of vibrating amplitudes with system size [Phys. Rev. Lett.: 117, 245701 (2016)] [Proc. Natl. Acad. Sci.: 114, 1850 (2017)] [Proc. Natl. Acad. Sci.: 112, 1856 (2017)] . Periodicity is not a prerequisite for the arguments about the lack of global symmetry breaking given by Bloch, Peierls, and Landau: one of the most prominent starting points for the unusual behaviour of low dimensional ensembles is also relevant in amorphous solids (and certainly in 2D quasi-crystals). The logarithmic divergence was found in surprisingly small ensembles, again highlighting soft matter systems as being ideally suited to investigate fundamental issues of statistical physics. In atomic ensembles, monolayers of astronomic [Phys. Rev. Lett: 44, 463 (1980)] , or at least continental size [Nat. Mat.: 6, 858 (2007)] [Europhys. Lett. Lett: 85, 46002 (2009)] would be necessary to measure a significant signature of Mermin-Wagner-Hohenberg fluctuations. Our contribution to this field was highlighted in PNAS [Proc. Natl. Acad. Sci.: 114, 2440 (2017)] and in Nature Physics, Research Highlights [Nat. Phys.: 13, 205 (2017)] .




