Experiementelle statistische Physik
Förderung im Heisenberg Programm der Deutschen Forschungsgemeinschaft
Kolloidale Ensemble in zwei Dimensionen

Ich interessiere mich für Strukturbildung, Selbstorganisation, spontane Symmetriebrechung (in und fern des Gleichgewichtes) sowie den Übergang zu amorphen Festkörpern mit Fokus auf die zugrundeliegenden mikroskopischen Prozesse. Die Physik niedrigdimensionaler Systeme ist oft komplexer und zeigt eine größere Variation von angeregten Zuständen verglichen mit 3D Systemen. Die Beispiele hierfür reichen vom Quanten-Hall Effekt für 2D Elektronensysteme in MOSFET oder Dirac-Kegel der elektronischen Zustandsdichte in Graphen bis hin zu klassischen Systemen und ihrer Phasenübergänge in 2D. Lange Zeit existierten nur wenige analytische Theorien in 3D, wie z.B. das Sphärische Model [Phys. Rev.: 86, 821 (1952)] , die Übergangstemperaturen berechnen konnten, aber Renormierungsgruppentheorie ist zu einem mächtigen Werkzeug geworden [Phys. Rep.: 368, 549 (2002)]. In zwei Dimensionen ist in den Siebziger Jahren eine detaillierte Theorie entwickelt worden, die das Schmelzen mittels topologischen Defekten und der dazugehörigen Renormierung der Elastizität beschreibt. Diese sogenannte Kosterlitz-Thouless-Halperin-Nelson-Young-Theorie (in Kürze KTHNY-Theorie) [J. Phys. C: 5, L124 (1972)] , [J. Phys. C: 6, 1181 (1973)], [Phys. Rev. Lett: 41, 121 (1978)], [Phys. Rev. B: 19, 2457 (1979)], [Phys. Rev. B: 19, 1855 (1979)], ist jüngst einem breiten Publikum bekannt geworden: Michael Kosterlitz und David Thouless haben 2016 für ihren Beitrag zur Theorie für 2D Schmelzen den Nobelpreis für Physik erhalten.
Mit einem kolloidalen Ensemble (das ist eine Monolage von mesoskopischen Partikeln, die Brownsche Bewegung vollführen) haben wir erfolgreich alle Vorhersagen der KTHNY-Theorie geprüft. Mike Kosterlitz hat in seinem Nobelvortrag unsere experimentellen Arbeiten zu topologischen Phasenübergängen hervorgehoben [Rev. Mod. Phys.: 89, 040501 (2017)] : "One of the main measurable predictions of the dislocation theory of melting is the renormalized (measured) Young’s modulus for which there is remarkable agreement between experiment and theory as shown in Fig. 5. Although the theoretical predictions were made in the 1970s (Halperin and Nelson, 1978, 1979; Young, 1979), experimental measurements (Zanghellini, Keim, and von Grünberg, 2005; von Grünberg, Keim, and Maret, 2007) were not done for several decades because of the difficulties of realizing a suitable experimental system." (Siehe auch [https://www.nobelprize.org/uploads/2018/06/kosterlitz-lecture.pdf] - Fig. 5 des Nobelvortrages bekam die urheberrechtliche Abdruckgenehmigung aus [Jour. Phys. Cond. Matt.: 17, S3579 (2005)] : das "geeignete experimentelle System" welches Michael Kosterlitz nennt, ist die extrem gut equilibrierte und charakterisierte kolloidale Monolage, die wir in meiner Gruppe untersuchen.
Spontane Symmetriebrechung: Schmelzen in 2D und KTHNY-Theorie

Schon seit den 1930ern war unter anderem von Felix Bloch, Rudolf Peierls und Lew Landau diskutiert worden, ob Kristalle oder Magnetismus in zwei Dimensionen überhaupt existieren kann [Zeitschrift für Physik: 61, 206 (1930)] [Helv. Phys. Acta: 7, 81 (1934)] [Phys. Z. Sowj.: 11, 545 (1937)]. Der mathematisch exakte Beweis über das Fehlen von global gebrochenen Symmetrien in zwei Dimensionen ist im Mermin-Wagner-Hohenberg Theorem formuliert. Speziell für Kristalle in 2D zeigt es, dass die Auslenkungen von perfekten Gitterpositionen logarithmisch mit der Systemgröße über alle Grenzen wächst [Phys. Rev. Lett.: 17, 1133 (1966)] [Phys. Rev.: 176, 250 (1968)] [Phys. Rev.: 158, 383 (1937)]. Interessanterweise ist diese logarithmische Divergenz noch nie in 2D Kristallen gemessen worden - weder in kolloidalen Monolagen, noch in Graphen. Aber diese logarithmische Divergenz impliziert, dass es spontane Symmetriebrechung in 2D nicht geben kann. Diese Vorhersage ist oft dahingehend überinterpretiert worden, dass es folglich auch keine Kristalle in 2D geben kann. In der Tat war es der Wiederspruch zwischen genau dieser Interpretation des Mermin-Wagner-Hohenberg-Theorems und den Ergebnissen der ersten Computer-Simulationen von Alder und Wainwright, die Kristallisation in 2D fanden [Phys. Rev.: 127, 359 (1962)], der Michael Kosterlitz einst motivierte, als postdoc in der Gruppe von David Thouless über topologische Phasenübergänge zu arbeiten [Jour. Phys. Cond. Matt.: 28, 481001 (2016)]. Kosterlitz und Thouless sagten einen kontinuierlichen Phasenübergang (2. Ordnung) vorher, der durch topologische Defekte vermittelt wird, während andere Theorien und die ersten Computer Simulationen einen Übergang erster Ordnung vorhersagten [Phys. Rev. Lett.: 48, 933 (1982)]. Daraufhin ist der mikroskopische Mechanismus des Schmelzens in 2D über einige Jahrzehnte intensiv debattiert worden.
Auf den Arbeiten von Kosterlitz und Thouless aufbauend, haben David Nelson und Bertrand Halperin die Existenz einer hexatische Phase vorhergesagt, die als intermediäre Phase zwischen der isotropen Flüssigkeit und dem hexagonalen Kristall existieren soll. 2D Kristalle schmelzen derart mittels zweier kontinuierlicher Übergänge: Zwei Arten von topologischen Defekten (Dislokationen und Disklinationen) sorgen dafür, dass die Translations- und Orientierungssymmetrie bei unterschiedlichen Temperaturen gebrochen wird. Die hexatische Phase ist eine Art Flüssigkristall mit sechzähligem Direktorfeld und ist in 2D Kolloidsystemen gefunden worden [Phys. Rev. Lett.: 58, 1200 (1987)] [Phys. Rev. Lett.: 73, 3113 (1994)] [Phys. Rev. Lett.: 82, 2721 (1999)]. In der Tat sind die Übergänge kontinuierlich, wenn das System immer im thermischen Gleichgewicht gehalten wird. Unsere Ergebnisse unterstützen das zweistufige Schmelzen und die KTHNY-Theorie in allen vorhergesagten Aspekten und die kritischen Exponenten passen gut zu den Ergebnissen der Renormierungsgruppentheorie [Phys. Rev. E: 75, 031402 (2007)] [Chem. Phys. Chem.: 11, 963 (2010)]. Zusammen mit Computersimulationen haben wir sogar die spezifische Wärme des kolloidalen Ensembles bestimmt: Im Kristall haben wir Dulong Petits Gesetz nachgemessen; An den Übergangstemperaturen konnten wir zeigen, dass die spezifische Wärme durch die Dissoziation der topologischen Defekte und ihrer jeweiligen diskreten Core-Energie gegeben ist [Phys. Rev. Lett.: 113, 127801 (2014)] [Phys. Rev. Lett.: 95, 185502 (2005)].
Symmetriebrechung fern des Gleichgewichtes: Kibble-Zurek-Mechanismus
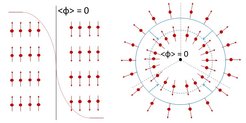
Fern des thermodynamischen Gleichgewichtes versagen die Methoden der klassischen Thermodynamik, um makroskopische Beobachtungsgrößen vorherzusagen. Anders als beim Schmelzen eines 2D Kristalles beobachten wir keine hexatische Phase im Experiment beim Einfrieren, wenn wir das System von der Hochsymmetriephase (isotrope Flüssigkeit) abkühlen. Dies wiederspricht der Annahme, dass Phasenübergänge reversibel sein müssen, wenn sie zwischen wohldefinierten thermodynamischen Zuständen vermitteln. Bei nichtverschwindenden Kühlraten beobachten wir in der symmetriegebrochenen Phase einen polykristallinen Kristall. Der theoretische Rahmen hierzu ist im sogenannten Kibble-Zurek-Mechanismus gegeben, der das Auftreten von topologischen Defektstrukturen wie Domänenwänden, Strings und Monopolen beschreibt, wenn das System bei endlichen Kühlraten durch einen kontinuierlichen Phasenübergang getrieben wird. Tom Kibble hat das Model ursprünglich für das primordiale Higgsfeld kurz nach dem Urknall entwickelt (inzwischen typischerweise Inflatonfeld genannt) [Jour. Phys. A: 9, 1387 (1976)] [Phys. Rep.: 67, 183 (1980)]. Wojciech Zurek hat es auf völlig anderen Skalen auf Quantenflüssigkeiten und Flüssigkristalle in kondensierter Materie angewandt [Nature: 317, 505 (1985)] [Phys. Rep.: 276, 177 (1996)]. Die jeweils beobachtbaren Defektstrukturen entstehen während des Abkühlens, wenn räumlich getrennte Regionen nicht nach dem Einsteinschen Kausalitätsprinzip verbunden sind: Gebiete, die so weit voneinander entfernt sind, dass sie nicht über ihre lokale Symmetrie "kommunizieren" können, können nicht notwendig denselben Ordnungsparameter während der spontanen Symmetriebrechung annehmen. In der Kosmologie ist die endliche Signalgeschwindigkeit ultimativ durch die Lichtgeschwindigkeit multipliziert mit der Expansionsrate des Universums gegeben, was einen kosmischen Ereignishorizont beim gegebenen Alter des Universums definiert. In kondensierter Materie ist die endliche Signalgeschwindigkeit durch die Schallgeschwindigkeit gegeben (bzw. zweiter Schall in suprafluidem Helium) was einen "akustischen Horizont" definiert. Wenn mit endlichen, nichtverschwindenden Raten gekühlt wird, entstehen separierte Domänen mit unterschiedlichen Werten des lokalen Ordnungsparameters. Wir konnten zeigen, dass die typischen Längenskalen des Netzwerkes aus Defekten als Funktion der Kühlrate exakt dem Kibble-Zurek-Mechanismus folgen, wenn dieser auf die Kosterlitz-Thouless Universalitätsklasse angewendet wird. [Proc. Natl. Acad. Sci.: 112, 6925 (2015)]. Derart zeigt unsere kolloidale Monolage faszinierende Ähnlichkeiten wie Quantenflüssigkeiten und sogar mit dem primordialen Higgsfeld in Urknalltheorien. Die Analogien zwischen diesen recht unterschiedlichen Systemen stammen vom zweikomponentigen Ordnungsparameter, den sie alle gemeinsam haben. Diese Arbeit ist in PNAS kommentiert [Proc. Natl. Acad. Sci.: 112, 6780 (2015)] und mit dem Gustav-Hertz-Preis der Deutschen Physikalischen Gesellschaft gewürdigt worden.
Amorphe Systeme und Vitrifikation

Andere Systeme, die fern des Gleichgewichtes sind, sind Gläser. Die "Technologie" der Menschheit fing im Steinzeitalter vor mehr als einer Million Jahre mit der Nutzung von glasartigen Materialien wie dem Obsidian an, um die ersten primitiven Werkzeuge wie den Faustkeil zu schaffen. Dennoch gibt es nach wir vor keine theoretische Beschreibung von Gläsern, die alle experimentell beobachteten Phänomene während des Glasübergangs beschreiben kann. Vom technologischen Standpunkt aus, wird eine unterkühlte Flüssigkeit Glass genannt, wenn ihre Viskosität 1012 Pa·s überschreitet - unabhängig davon ob sie danach endlich bleibt oder an einem idealen Glasübergang divergiert [Nature: 410, 259 (2001)]. Für schnelle Kühlraten ist dieser Schwellwert bei einer höheren Temperatur erreicht, während er für langsame Kühlraten erst bei einer niedrigeren Temperatur erreicht wird. Die Übergangstemperatur TG hängt von der Vorgeschichte ab und folglich trennt der Glasübergang keine wohldefinierten thermodynamischen Phasen. Während die Modenkopplungstheorie eine dynamische Bifurkation als Funktion der Temperatur vorhersagen kann, indem sie Integrodifferentialgleichung von korrelierten Dichtefluktuationen löst, erklären andere Modelle wie z.B. die "Random First Order Transition" den Glasübergang mit einem zugrundeliegenden Phasenübergang, der wegen der divergierenden Viskosität nie erreicht wird. Divergierende Viskositäten implizieren jedoch divergierende Relaxationszeiten - und diese zeitlichen Divergenzen sind im Experiment oder in Computersimulationen schwierig zu greifen. Während Viskositäten auf Seiten der Flüssigkeit die relevanten Observablen sind, enthalten Elastizitäten komplementäre Information auf der Festkörperseite. Um die divergierenden Relaxationszeiten zu vermeiden, haben wir deswegen die elastischen Eigenschaften eines kolloidalen Glases experimentell in der Nähe des Glasübergangs untersucht: Unsere Ergebnisse zeigen, dass sich die Scherelastizität am Glasübergang diskontinuierlich verhält. Dies bestimmt die Glasübergangstemperatur eineindeutig [Phys. Rev. X: 5, 041033 (2015)] und adressiert fundamentale Fragen über die Elastizität von Gläsern am Übergang, nämlich das kontinuierliche [Phys. Rev. Lett: 105, 015504 (2010)] gegenüber dem diskontinuierlichen Verhalten bei TG [Phys. Rev. Lett.: 107, 105505 (2011)] [Phys. Rev. Lett: 109, 178301 (2012)].
Langwellige Instabilitäten: Goldstone-Moden und das Mermin-Wagner-Theorem
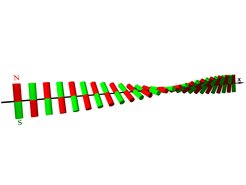
Inzwischen ist es gut etabliert, dass sich die Kristallisation in zwei und drei Dimensionen signifikant unterscheidet. Ob der Glasübergang von der Dimensionalität abhängt, ist eine offene Frage. Interessanterweise gibt es Theorien, die einen idealen Glasübergang (mit echten Divergenzen der Viskosität) in unendlich vielen Dimensionen vorhersagen [Jour. Stat. Mech.: 2012, P10012 (2012)]. In 2015 haben Ergebnisse von umfassenden Computersimulationen des Glasübergangs von Unterschieden zwischen 2D und 3D Systemen berichtet. Der Übergang war in 2D weniger deutlich ausgeprägt als in 3D und eine Entkopplung der Translations- und Orientierungsfreiheitsgrade wurde in 2D gefunden, aber nicht in 3D [Nat Comm.: 6, 7392 (2015)]. Daraus wurde geschlossen, dass sich die mikroskopischen Szenarien des Glasübergangs in 2D und 3D unterscheiden. Die in den Simulationen gefundenen Unterschiede können jedoch auch mit langwelligen Fluktuationen der Translationsfreiheitsgrade vom Mermin-Wagner-Hohenberg-Typ erklärt werden, die eigentlich für das Fehlen eines globalen Symmetriebruchs in 2D Kristallen verantwortlich sind. Zusätzlich können sie die phänomenologischen Unterschiede bei 2D und 3D Gläsern erklären, ohne dass notwendig das mikroskopische Szenario unterschiedlich sein muss.
Indem wir Daten von 2D kolloidalen Kristallen, 2D kolloidalen Gläsern, 3D kolloidalen Gläsern und 2D Computer Simulationen verglichen, konnten wir die Existenz von Mermin-Wagner-Hohenberg-Fluktuationen in 2D amorphen Festkörpern klar nachweisen. In den Computersimulationen war es zusätzlich möglich den "Fingerabdruck" der Mermin-Wagner-Hohenberg-Fluktuationen nachzuweisen, nämlich die logarithmische Divergenz der Amplitude von akustischen Moden mit der Systemgröße [Phys. Rev. Lett.: 117, 245701 (2016)] [Proc. Natl. Acad. Sci.: 114, 1850 (2017)] [Proc. Natl. Acad. Sci.: 112, 1856 (2017)]. Offensichtlich ist Periodizität keine Voraussetzung für die Argumente über das Fehlen von globalen Symmetriebrüchen, wie sie von Bloch, Peierls und Landau diskutiert wurden: Einer der prominentesten Ausgangspunkte für das besondere Verhalten von niedrigdimensionalen Systemen ist auf in amorphen Festkörpern relevant (und sicherlich auch in 2D Quasikristallen). Zugleich wurde die logarithmische Divergenz in erstaunlich kleinen Systemen gefunden; Ensembles aus "Weicher kolloidaler Materie" sind offensichtlich ideal geeignet, fundamentale Fragestellungen der statistischen Physik zu addressieren. In atomaren Systemen wären Monolagen von astronomischer In atomic ensembles, monolayers of astronomic [Phys. Rev. Lett: 44, 463 (1980)] , oder zumindest kontinentaler Ausdehnung nötig [Nat. Mat.: 6, 858 (2007)] [Europhys. Lett. Lett: 85, 46002 (2009)] um eine signifikante Signatur von Mermin-Wagner-Hohenberg-Fluktuationen zu messen. Unsere Beiträge zu diesem Thema sind in PNAS [Proc. Natl. Acad. Sci.: 114, 2440 (2017)] und in Nature Physics, Research Highlights [Nat. Phys.: 13, 205 (2017)] kommentiert worden.




