
Kollektive Phänomene fern vom Gleichgewicht
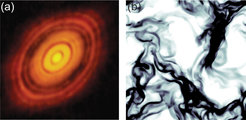
Symmetriebrechung und Strukturentstehung sind weit verbreitete und extreme wichtige kollektive Phänomene, die fern vom thermischen Gleichgewicht stattfinden. Wohlbekannte Beispiele sind schwärmende Stare [1,2], Muster in Bakterienkolonien [3], Filamentbildung in Kolloidsuspensionen [4], thermische Konvektion [5,6], oder auch die Stop-and-go-Wellen in einem Verkehrsstau [7]. Ein besonders altehrwürdiges Beispiel ist das Verklumpen kosmischen Staubs in den Akkretionsscheiben um junge Sterne (cf. Fig. 1a), führt es doch schließlich zur Entstehung von Planeten wie etwa Erde, und somit gelegentlich zur Entstehung von Leben und unserer selbst.
Für Systeme nahe dem Gleichgewicht kann man sehr genau angeben, wohin es sich entwickeln will, nämlich zum Minimum der Freien Energie. Diese läßt sich im Prinzip nach wohlbekannten Rezepten aus den mikroskopischen Eigenschaften des Systems berechnen. Für Systeme fern vom Gleichgewicht aber, und das sind die meisten und die interessantesten, gibt es kein vergleichbares Analogon zur Freien Energie. Etwas ähnliches zu haben wäre sehr praktisch, denn es würde erlauben, vorherzusagen, welche Strukturen ein System zu entwickeln imstande ist und welche davon am wahrscheinlichsten entsteht. Ilya Prigogine dachte, er könne ein solches Prinzip über den Begriff der Entropieproduktion formulieren [8]. Als er dafür 1977 den Nobelpreis für Chemie bekam, war allerdings schon bewiesen worden, daß sein Ansatz falsch war [9,10]. Mehr noch: daß, wenn es ein solch allgemeines Prinzip geben sollte, es jedenfalls nicht durch die Entropieproduktion ausgedrückt werden kann. Seither sind viele vergebliche Versuche unternommen worden, allgemeine Gesetzmäßigkeiten zu finden, nach denen ein System seinen stationären Nichtgleichgewichtszustand findet.
Wir haben hierzu einen eigenen Weg eingeschlagen, der recht vielversprechend aussieht und der darauf beruht, daß man nicht die Klasse aller möglichen Zustände des Systems untersucht, sondern die Klasse aller möglichen Rundreisen (Zyklen) in diesem Zustandsraum. Das Besondere ist nämlich, daß für die Übergangsraten zwischen diesen Zyklen detaillierte Bilanz gilt, eine wichtige Eigenschaft, die sonst nur in Gleichgewichtssystemen zu finden (und für deren Behandelbarkeit entscheidend) ist. In dem sonst üblicherweise diskutierten Bild der (diskreten) Mastergleichung nützt das nichts, wie sich bei näherer Betrachtung herausstellt, aber im Bild der (kontinuierlichen) Fokker-Planck-Gleichung lassen sich die Übergangsraten tatsächlich aus mikroskopischen Daten allein (dem Diffusionsfeld und dem Driftfeld) durch Integration berechnen. Man gelangt schließlich zu einer Methode, bei der das Verhalten des Systems durch die statistischen Gewichte der invarianten Mannigfaltigkeiten seines Driftfeldes beschrieben wird.
Über diese sehr fundamentalen Betrachtungen hinaus untersuchen wir experimentell, theoretisch und durch Simulation eine ganze Reihe von Systemen fern vom Gleichgewicht, die uns helfen sollen, ein besseres allgemeines Verständnis von Nichtgleichgewichtsphänomenen zu bekommen. Hierzu gehören granulare Gase, deren Verklumpen ein besonders gut experimentell und simulativ behandelbares Phänomen darstellt (Fig. 1b). Hier sind die Stöße der Partikel dissipativ, die entstehenden Strukturen werden getrieben und bestimmt vom Energiefluss aus der kinetischen Energie der Partikel in deren thermische (d.h. atomare) Freiheitsgrade.

Etwas komplexer sind Systeme aus aktiven Partikeln, wie etwa Plankton, das sich aktiv schwimmend fortbewegt, und dessen Verhalten in nichttrivialen Geometrien einige Überraschungen bereit hält. Als Modellsystem für das Schwarmverhalten aktiver Partikel kommen werden auch Emulsionen aus selbstschwimmenden Tröpfchen untersucht, an denen sich z.B. der Einfluss der Dimensionalität des Gesamtsystems auf das kollektive Verhalten gut studieren läßt (Fig. 2a). Besonders komplex, aber im Ergebnis auch von besonderer Eleganz, sind einzellige Algen, die Filamente bilden. Hier stapeln sich die einzelnen (etwa zylindrischen) Zellen zu langen Säulen, deren Länge ein vieltausendfaches ihres Durchmessers erreichen kann. Diese säulenhaften Filamente kriechen (durch einen bislang unbekannten Mechanismus) über eine Unterlage, etwa eine Agar-Platte, mit einer Geschwindigkeit von einigen µm pro Sekunde, und zwar stets entlang des von ihrer Achse vorgezeichneten Pfades. Zwingt man sie nun in zwei Dimensionen, indem man sie zusätzlich mit einer Glasplatte - im Abstand eines Filamentdurchmessers vom Substrat - abdeckt, so entstehen breite Flöße, deren Bewegung wirkt wie gigantische Verkehrsströme auf Autobahnen mit hunderten von Spuren (Fig. 2b).
Auch reale Verkehrssysteme können als aktive Fluide betrachtet werden. Angesichts der Tatsache, dass die wichtigste Frage unserer Zeit ist, wie der Mensch seine ökologische Nische auf dem Planeten Erde nachhaltig gestalten kann, bietet es sich an, daß wir unsere Erkenntnisse über aktive Materie und kollektives Verhalten fern vom Gleichgewicht auf sozio-ökonomische Systeme anwenden und versuchen, zu praktischen Lösungen beizutragen. Beispielsweise konnten wir zeigen, daß bedarfsgetriebene Ride-Sharing-Dienste im typischen, vom Privatauto dominierten Marktgeschehen einen diskontinuierlichen Phasenübergang aufweisen. Die „Phasen“ entsprechen zwei stabilen Fixpunkten in der Marktdynamik. Der eine korrespondiert zu dem üblichen "Tal des Jammers" der meisten Ride-Sharing-Systeme, die einen Nischenmarkt bei hohem Preis bedienen [11]. Es gibt aber eben, in einem weiten Parameterbereich, einen zweiten Fixpunkt, bei dem Ride-Sharing den Markt vollkommen dominiert (Fig. 2c). Wir erarbeiten durch Theorie, Simulation und Experiment (Pilotprojekte) ein tieferes Verständnis solcher Systeme, auch im Bereich Multimodalität, der für die Mobilität der Zukunft sicher eine große Rolle spielen wird.
Wer an einer detaillierteren Darstellung interessiert ist, kann hier auf Erdisch weiterlesen.
Literatur
[1] M. Ballerini, N. Cabibbo, R. Candelier, A. Cavagna, E. Cisbani, I. Giardina, V. Lecomte, A. Orlandi, G. Parisi, A. Procaccini, M. Viale and V. Zdravkovic, P.N.A.S. 105 (2008) 1232.
[2] A. Attanasi, A. Cavagna, L. Del Castello, I. Giardina, T. S. Grigera, A. Jelić, S. Melillo, L. Parisi, O. Pohl, E. Shen and M. Viale, Nat. Phys. 10 (2014) 691.
[3] E. Ben-Jacob, I. Cohen and H. Levine, Adv. Phys. 49 (2000) 395.
[4] T. Vissers, A. Wysocki, M. Rex, H. Löwen, C.P. Royall, A. Imhofa and A. van Blaaderena, Soft Matter 7 (2011) 2352.
[5] C.W. Meyer, G. Ahlers and D.S. Cannell, Phys. Rev. Lett. 59 (1987) 1577.
[6] M.C. Cross and P.C. Hohenberg, Rev. Mod. Phys. 65 (1993) 851.
[7] D. Helbing, Rev. Mod. Phys.73 (2001) 1067.
[8] P. Glansdorff and I. Prigogine, Thermodynamic theory of structure, stability, and fluctuations (Wiley, London 1971).
[9] J. Keizer and R.F. Fox, P.N.A.S. 71 (1974) 192.
[10] R. Landauer, Phys. Rev. A 12 (1975) 636.
[11] C. Mehlert, Schriftenreihe für Verkehr und Technik 91 (2001) 1.

