Fracture
Solids break, if stressed sufficiently. It is often a question of survival (stability of aero-planes, buildings, bridges) and sometimes that of profit (natural reserve extraction from underground) to understand the failure properties of materials. However, it is the question of universality and simple generic modeling of such failures that primarily motivate the following studies.
In particular, my colleagues and I worked on numerical simulations and partly analytical calculations of discrete models of fracture and failure problems in disordered systems. The models include random fiber bundle model, the spring-block train model for earthquakes and elastic interface driven through disordered media [1,4].
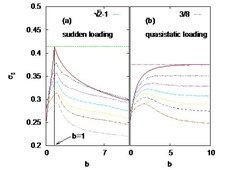
- In a general framework for failure of disordered system, we looked at the possibility of maximizing the strength of the system by tuning the load redistribution following a local failure. We could obtain theoretical limits of such strengths and propose ways to achieve the limit [5]. The figure shows the variation of the strength of the system with some tuning parameter of the redistribution rule for complete and partial knowledge of the individual failure thresholds.
- The mode of failure in disordered solids depends on the spread of disorder and range of interaction controlling the stress nucleation. In fiber bundle model, we could arrive at a scaling criterion, linking the range of interaction to the system size, which can predict the failure modes in different variants of the model [3].
- Other than investigating the many intriguing features of these models (see publications for details) we also attempt to find the universality in their behaviour in terms of the criticality observed in these models. We could do that for train model of earthquake and driven elastic interface [2]. This in general helps in clarifying the underlying physical processes in these apparently different models.
Selected publications
1. Statistical physics of fracture, friction and earthquakes, Hikaru Kawamura, Takahiro Hatano, Naoyuki Kato, Soumyajyoti Biswas and Bikas K. Chakrabarti, Rev. Mod. Phys. 84, 839 (2012).
2. Equivalence of the train model of earthquake and boundary driven Edwards-Wilkinson interface, Soumyajyoti Biswas, Purusattam Ray and Bikas K. Chakrabarti, Eur. Phys. J. B 86, 388 (2013).
3. Nucleation versus percolation: Scaling criterion for failure in disordered solids, Soumyajyoti Biswas, Subhadeep Roy and Purusattam Ray, Phys. Rev. E 91, 050105(R) (2015).
4. Statistical physics of fracture, breakdown and earthquake, Soumyajyoti Biswas, Purusattam Ray and Bikas K. Chakrabarti, John Wiley and sons (2015).
5. Maximizing the strength of fiber bundles under uniform loading, Soumyajyoti Biswas and Parongama Sen, Phys. Rev. Lett. 115, 155501 (2015).
