DEPARTMENT OF FLUID PHYSICS, PATTERN FORMATION AND BIOCOMPLEXITY
Wall Roughness Effects

Wall Roughness Effects

Surface roughness is known to have a large impact on the global heat transfer. Therefore we study numerically the effect of the roughness introduced by a set of distinct obstacles attached to the heating and cooling plates, for different Rayleigh and Prandtl numbers, and configurations of the cell geometry.

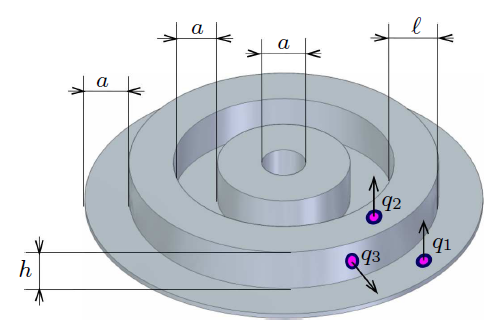
In our recent work Emran, et al., J. Fluid Mech. 882 (2020), A3, we investigate the influence of the regular roughness of the heated and cooled plates on the mean heat transport in a cylindrical Rayleigh–Bénard convection (RBC) cell of the aspect ratio one. The roughness is introduced by a set of isothermal obstacles, which are attached to the plates and have a form of concentric rings of the same width. The considered Prandtl number Pr equals 1, the Rayleigh number Ra varies from 106 to 108, the number of the rings on each plate is 1, 2, 4, 8 or 10, the height of the rings is varied from 1.5% to 49% of the cylinder height and the gap between the rings is varied from 1.5% to 18.8% of the cell diameter.

Temperature iso-surface and streamlines for Ra=107, a/H=0.25 and n=4 (notations are illustrated below).

The choice of the geometry is motivated by the following reasons. In cylindrical domains with ring-shaped roughness elements, the turbulent wind, or the large-scale circulation (LSC) that develops in RBC cells for sufficiently large Ra, unavoidably goes across the roughness elements, independently from the LSC orientation. Also the choice of such geometry is motivated by a reduced influence of the sidewall effects compared to the previously studied case of convection in box-shaped containers with small widths.

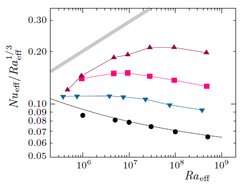
DNS show that by small Ra and wide roughness rings, a small reduction of the mean heat transport (the Nusselt number Nu) is possible, but in the most cases, the presence of the heated and cooled obstacles generally leads to an increase of Nu, compared to the case of classical RBC with smooth plates. When the rings are very tall and the gaps between them are sufficiently wide, the effective mean heat flux can be several times larger than in the smooth case. For a fixed geometry of the obstacles, the scaling exponent in the Nu vs. Ra scaling first increases with growing Ra up to approximately 0.5, but then smoothly decreases back towards the exponent in the no-obstacle case.

Bottom plate of a cylindrical container with 2 regular concentric ring-shaped obstacles, where a is the gap between two neighbouring rings, l is the width of each ring and h is the height of each ring (left). Snapshot of the temperature iso-surface. Case: Ra=107, h/H=0.25, a/H=0.10 with 4 rings, where H is the height of the cylinder. Pink represents hot and blue represents cold fluid (right).

Snapshots of the flow fields in the central vertical cross-sections, for 107, the number of the ring-shaped obstacles n = 4, the gap between the obstacles a/H = 0.10 and the obstacle height (a) h/H = 0.015, (b) h/H = 0.25 and (c) h/H = 0.4.
Dependences of the normalised effective Nusselt number Nueff on the effective Rayleigh number Raeff and for the obstacle height h/H = 0.12 and the obstacle gap a/H = 0.18 and the number of the ring-shaped obstacles n = 1 (down-pointing triangles), a/H = 0.18 and n = 2 (squares) and a/H = 0.10 and n = 4 (up-pointing triangles). For comparison are also shown: the predictions of the theory by Grossmann & Lohse (2000, 2001) with the coefficients from Stevens et al. (2013) (black curve) and the slope Nueff ~ Raeff1/2 (grey stripe) and the DNS data for the classical RBC in a cylinder of the aspect ratio=1, Pr = 1 and smooth plates (closed circles).

Further reading

Mohammad Emran, Olga Shishkina. Natural convection in cylindrical containers with isothermal ring-shaped obstacles. J. Fluid Mech. 882 (2020), A3.
 
Xiaojue Zhu, Richard J.A.M Stevens, Olga Shishkina, Roberto Verzicco, Detlef Lohse. Nu~Ra1/2 scaling enabled by multiscale wall roughness in Rayleigh–Bénard turbulence. J. Fluid Mech. 869 (2019), R4.
 
Sebastian Wagner and Olga Shishkina. Heat flux enhancement by regular surface roughness in turbulent thermal convection J. Fluid Mech. 763 (2015), 109–135.

Web-View
Print Page
Open in new window
Estimated DIN-A4 page-width
Go to Editor View