
Rayleigh–Bénard Turbulence
Turbulent thermal convection is ubiquitous in nature – occurring in the planets' oceans, atmospheres and mantles, as well as in stars, including our Sun. Convective heat transport is also important in engineering and technological applications. Rayleigh–Bénard convection (RBC) is one of paradigm systems to study turbulent thermal convection. In a RBC cell, a fluid is confined between two horizontal plates, an upper cooled and a lower heated, and adiabatic vertical walls. All processes inside the RBC cell are determined mainly by the dimensionless Rayleigh number Ra and the Prandtl number Pr, which both depend on the fluid properties, and Ra is also proportional to the cubed cell height and to the temperature drop between the highest and lowest temperature in the system.
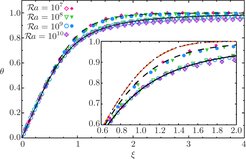
Viscous and thermal boundary layers (BLs) play a critical role in the heat transfer. The classical BL Prandtl–Blasius–Pohlhausen theory cannot describe well the BLs in turbulent RBC as its inherent features like pressure gradients within the BLs, fluctuations and buoyancy, are assumed to be negligible in that approach. Therefore in Shishkina et al., Phys. Rev. E 89 (2014) and Shishkina et al., J. Fluid Mech. 730 (2013) we advanced the BL theory by its extension to the case of a non-vanishing pressure gradient within the BLs, when a large-scale circulation approaches the heated and cooled plates not parallel to them. Further, in Shishkina et al., Phys. Rev. Lett. 114 (2015) we studied the effect of fluctuations within the BLs by considering the turbulent thermal diffusivity κτ there. We derived that in the vicinity of the plates, κτ is a cubic function on the vertical coordinate ξ, and only later, for larger ξ, where the velocity and temperature profiles start to follow a log-law, κτ is almost linear on ξ. The new developed BL equations were solved analytically for the case of infinitely large Prandtl number Pr and Pr ∼ 1 (see figure below) and an excellent agreement with direct numerical simulations was demonstrated.
In Shishkina et al., Phys. Rev. Fluids 2 (2017), based on an analysis of self-similarity of the boundary layer equations, we derived the scaling relations of the Nusselt number and Reynolds number with the Rayleigh number and Prandtl number in the limiting large-Prandtl-number regime of the scaling theory by Grossmann and Lohse.
Further reading
Emily S. C. Ching, H. S. Leung, Lukas Zwirner, Olga Shishkina. Velocity and thermal boundary layer equations for turbulent Rayleigh–Bénard convection. Phys. Rev. Research 1 (2019), 033037.
Olga Shishkina, Susanne Horn, Mohammad Emran, Emily S. C. Ching. Mean temperature profiles in turbulent thermal convection. Phys. Rev. Fluids 2 (2017), 113502.
Olga Shishkina, Mohammad Emran, Siegfried Grossmann, Detlef Lohse. Scaling relations in large-Prandtl-number natural thermal convection. Phys. Rev. Fluids 2 (2017), 103502.
Emily S. C. Ching, On-Yu Dung, Olga Shishkina. Fluctuating thermal boundary layers and heat transfer in turbulent Rayleigh–Bénard convection. J. Stat. Phys. 167 (2017), 626–635.
Olga Shishkina, Susanne Horn, Sebastian Wagner, Emily S. C. Ching. Thermal boundary layer equation for turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 114 (2015), 114302.
Olga Shishkina, Sebastian Wagner, Susanne Horn. Influence of the angle between the wind and the isothermal surfaces on the boundary layer structures in turbulent thermal convection. Phys. Rev. E 89 (2014), 033014.
Olga Shishkina, Susanne Horn, Sebastian Wagner. Falkner–Skan boundary layer approximation in Rayleigh–Bénard convection. J. Fluid Mech. 730 (2013), 442–463.
