
Research Karpitschka group
Self-Organization of Living Polymeric Matter

What is “living polymeric matter”? Imagine a bowl of pasta coming to life, each spaghetti gliding along its contour through the entangled mess of its siblings. What we actually study isn’t pasta, but looks similar when observed under a microscope: filamentous cyanobacteria. These are truly fascinating organisms that form long filaments, indeed a bit like tiny green spaghetti that move on top of each other. And they’re alive, actually since over two billion years, as far as we can tell from their fossil record. That means they have survived all the climates that our planet went through, from snowball earth to the hot phases when dinosaurs felt comfy. Even more, they “made” climate because of their photosynthetic activity, using light to convert carbon dioxide into biomass and oxygen. This caused the great oxygenation event, the biggest climate catastrophe in the history of our planet, over two billion years ago.
Here, “catastrophe” is from cyanobacteria’s point of view; we actually breathe the oxygen they made. But we also burn their remainders, fossil fuels, causing the exact inverse, a “great oxidation event” (another climate catastrophe, this time, from our point of view). But they survived their catastrophe, so we can learn from them how they managed. And that’s exactly what we want to find out. The key message is simple: Together they were strong! Individual cells could not have survived such vastly different conditions, but as a colony of millions of filaments, they could adapt, simply by changing the shape of their colony. A compact sphere with minimal surface when facing too much light, but spreading out and collecting the very last photons when volcanoes darkened the skies. What we don’t understand is how this works: Since they are simple organisms, not capable of “thinking”, they must rely on the principles of self-organization i.e., what emerges naturally in an ensemble of simple, yet responsive filaments.
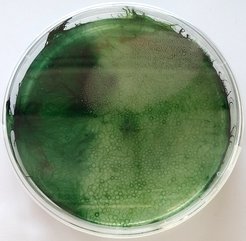
This is where our research starts: we quantify their active and passive mechanical properties and the responses that individual filaments show to stimuli, under varying culture conditions. At the same time, we observe the colony architectures and their macroscopic physico-chemical properties that form in these varying culture conditions. To learn about the hierarchy of mechanisms that leads from the small end to the large end, we use an old trick: We place them into artificial environments, reducing their freedom to move and organize, and thereby isolate the mechanisms at play, to study them one by one. Apart from the beauty of their ballet, we might actually get a better clue how to use and tame them, to cope with the blooms they form in our lakes and oceans, and use them as a renewable energy source.
Interfacial Singularities
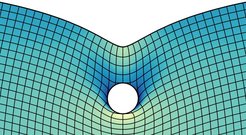
What is a singularity? If we describe a physical phenomenon with a continuum theory, like the adhesion of a flat elastic material to a rigid sphere, we frequently observe that a physical quantity, in this case the stress in the solid, becomes infinitely large at some “singular point”. Here the singular point is the edge of the contact. In nature however, nothing becomes truly infinite, so there must be something wrong with the continuum theory. Obviously, the equations did not take into account the discrete (atomic) nature of materials. But fully describing all atoms is a formidable task, because there’s so many of them – how could we “save” continuum theory, and take microscopic physics into account? Here are a few recent discoveries that illustrate our research in this field.

The concept of surface tension is one example: molecules in the bulk of a liquid interact with each other on all sides. The molecules at the interface to a gas are missing half of their interaction partners. This causes surface tension, which can be included in continuum theories. Scientists agree that surface tension is utterly important to describe liquids. For solids, surface tension was largely ignored in the past because there, the consequences are much smaller due to the rigidity of a solid. But approaching a singularity, it becomes important again. The distance below which solid surface tension matters can be calculated by comparing surface tension to stiffness, ɣ/E. This gives a length, the elastocapillary length. Within this range, the edge of an elastic contact is shaped by solid capillarity. After a couple of lines of variational calculus, one can show that surface tension also provides a boundary condition for the angle of contact between the elastic material and the sphere [Karpitschka et al., Soft Matter 12 (2016) 4463]. This is equivalent to what is known for liquids as Young’s contact angle. On small scales, adhesion and wetting are equivalent!
Compressing a slice of soft bread, one can observe an inward fold with a self-contacting surface of the bread. A very similar effect is responsible for the morphology of our brains, where an inward fold is termed “sulcus”. Sulci form because the outer part of the brain grows faster than the inner part. Despite its importance in biology and engineering, the morphology of such inward-folds, in mechanics called creases, remained unexplored. In our paper [Karpitschka et al., Phys. Rev. Lett. 119 (2017) 198001] we discovered a continuous precursor to a crease, a “furrow”: it can be generated by deforming a soft surface inward, for instance by deflating a liquid inclusion beneath the surface, or pulling a solid inclusion downward. The furrow bifurcates sub-critically into a crease, when the surface region becomes compressed beyond a critical point: The free surface folds upward into a self-contact. In the reverse direction, unfolding proceeds smoothly. Both, the furrow and the crease, are described by a simple mathematical concept: self-intersecting curves. The “simplest” set of curves that undergo self-intersection belongs to the universality class of “cusps”. When the radius of the surface reaches zero, it forms an interfacial singularity and folds. Of course, for a solid, self-intersection is replaced by a self-contact.
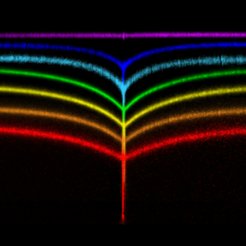
But what happens if the material is tacky? Tackiness is a consequence of compliance and adhesion i.e., that the material reduces its surface energy by snugly fitting onto the contacting body. In a “sticky crease”, this happens to a self-contacting surface. Surprisingly, we found that the micro-morphology at the edge of a self-contact changes drastically if the surface is tacky [van Limbeek et al., Phys. Rev. Lett. 127 (2021) 028001]: Instead of a gentle touch-down, we find a T-shape, with a sharp fold on either side of the opening contact. This is caused by surface tension, which is fully eliminated in the seemingly perfect contact, leaving no other option to balance forces. Similar to the contact between an elastic material and a sphere (see above), this “inner region” is dominated by solid capillarity, making it similar to the wetting of a liquid on a solid surface. We could even recover the typical behavior of liquids that spread or recede on imperfect surfaces, but this time, for a closing or opening self-contact: The contact edge is subject to contact line pinning, meaning that the history of the contact matters: Creases look different during folding and unfolding.
Evaporating Multi-Component Droplets
Sessile droplets typically evaporate faster near their edge than at their center. In droplets that consist of only one single liquid, capillarity compensates these losses, causing a strong flow toward the edge of the droplet. This is the reason why coffee-stains look like rings: coffee particles move with the capillary flow and are deposited in a ring around the droplet. If, however, a solute or a second, less volatile liquid is present in the droplet, this component will enrich near the edge of the droplet. In contrast to inert particles, however, liquids or solutes influence surface tension, which is why their local enrichment causes another type of flow, known as Marangoni convection. It can be directed toward the contact line, or away from it, depending whether the residual component increases or decreases the surface tension, respectively. Both cases are equally important, and applications range from printing to cleaning. We work on a quantitative understanding and try to reveal underlying universal concepts and scaling laws that allow to predict the behavior of droplets in technological applications.
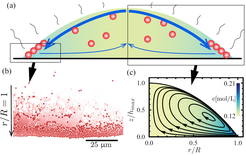
For salty droplets, surface tension increases near the edge of the droplet, and salt enrichment in this region causes ring-shaped corrosion stains on stainless steel surfaces [Soulie et al., PCCP 17 (2015) 22296]. If the contact line of the droplet is pinned i.e., it is not free to move, the outward Marangoni flow is compensated by a Capillary flow, leading to a quasi-stationary droplet shape and flow pattern. Intriguingly, if particles are present, this flow pattern causes another kind of ring-shaped deposit that is different from the classical coffee-stain: Instead of accumulating in bulk form, particles assemble into ordered monolayers at the free surface of the liquid. Due to the ongoing evaporation, the layer is then deposited onto the substrate. Controlling this effect is important in ink-jet printing, but, thinking further, one could possible use this effect to create large ordered layers of particles that serve as photonic crystals [Marin et al., Phys. Rev. Fluids 4 (2019) 041601(R)].
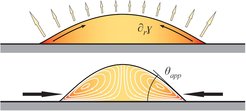
If this flow is directed the other way round, e.g. as for glycerol/water mixtures, and if the pure liquids wet the substrate, these flows even dominate the shape of the droplet: instead of spreading and covering the whole substrate, the liquids contract into a droplet with a stationary non-zero contact angle, as if the substrate would be non-wetting [Karpitschka et al., Langmuir 33 (2017) 4682]. Why is this important? Virtually any micro-electronic circuit, as in phones or computers, is made by wet processing and has to be dried at the end. So far, the wetting behavior of liquids on solids was known to be determined by the material’s surface energies (that’s Young’s law) and surface topography (Wenzel’s law), and nothing much could be changed about this. Drying microelectronics was (and is) a challenge, because material and topography are prescribed by the requirements of the electronics, not the drying; droplets would simply stick to the circuit. However, these contracted droplets seemingly forget about Young’s and Wenzel’s laws. Instead, their wetting behavior is governed by evaporation and can be controlled remotely by changing the atmospheric composition around the droplet [Karpitschka et al., Langmuir 33 (2017) 4682].
One may think that this effect can be enhanced simply by using more surface active components i.e., materials that reduce the tension of a surface by adsorbing to it. However, such materials frequently also adsorb to solid surfaces, causing another effect that changes the wetting behavior: autophobing. Adsorption to a solid forces the molecules into an orientation in which they expose their ‘tails’ that repel liquids. Even if the liquid is made of the very same molecules (simply because of the molecular orientation). Recently, we could show the coexistence of Marangoni contraction and autophobing, depending on ambient conditions [Hack et al., Langmuir 37 (2021) 3605]
Dynamical Elastocapillary Phenomena
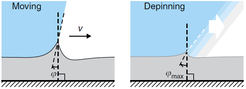
What happens if a localized deformation at the surface of a soft solid is forced to move? Consider, for example, a droplet that sits on top of an inclined soft solid: Capillary forces at the contact line act like a localized line force that pinches on the surface and deforms it into a sharp wetting ridge. Obviously, if the droplet slides down the soft surface, the deformation that it generates has to change over time. This causes dissipation, and it is not clear a priori what the shape of the solid will be, and which pattern the motion of the droplet will have. In my group, we investigate this problem, aiming at a fundamental understanding of cases where liquid and solid physics are strongly coupled together. In the following we give a few examples of our recent discoveries.

Previous experiments revealed that there are two distinct modes in which a contact line may move across a soft surface: one is a slow and continuous motion, that does not stop even at very small driving forces, allowing for velocities in the nanometer per second range. The other mode is a fast and irregular jumping motion, in which the velocity of the contact line fluctuates by orders of magnitude. Using the framework of linear elasticity we have calculated that, in the slow and steady mode, the wetting ridge is dragged along with the contact line, and dissipation in the solid makes it asymmetric. This asymmetry leads to a rotation of its tip, which allows to maintain a local balance between solid and liquid surface tensions [Karpitschka et al., Nature Commun. 6 (2015) 7891]. We could also shown that this must hold true in case one considers a balance of injected and dissipated power instead of local force balances [Karpitschka et al., PNAS 115 (2018) E7233]. In the fast, jumpy mode, the moving ridge is abandoned, the contact line surfs down its advancing face, and starts forming a new ridge on the slope of the old one.


Recently, we also managed to visualize the dynamical wetting ridge shapes with high spatio-temporal resolution [van Gorcum et al., Phys. Rev. Lett. 121 (2018) 208003]. This we achieved with a little trick that gave us optical access to the ridge: instead of using a flat substrate, we made a cavity in a block of polymer gel held by a cuvette, such that the wetted surface could be observed through the (transparent) solid. With this technique, we made a very intriguing discovery: Not only the ridge rotates, but also its opening angle depends on velocity. This is unexpected because it can only originate in a change in one of the surface tensions. It turned out that this is most likely the surface tension of the solid. It is well known that the surface tension of a solid may change if the surface is stretched, an effect that does not exist for pure liquids. It does, however, have an analogy in the world of liquid surfaces, which is a surfactant-covered surface: expansion of the surface decreases coverage, and hence surface tension increases. Due to the dissipation-induced shape change of the ridge, the surface experiences a velocity-dependent stretch. However, there are indications that this is not sufficient to explain our observation: In addition to strain-dependence, the surface should follow its own, distinct rheology.
A closely related case is peeling a flexible strip off a soft, elastic adherent material. For strong adhesives, this delamination process is governed by cavitation and fibril formation, which is highly nonlinear and hard to model quantitatively. However, “weak” or rather “reversible” adhesives become increasingly important in daily applications (think about post-its, for example) because adhesion and peeling can be repeated many times. Now the adherent part of the substrate is coupled to the bending rigidity of the tape, in contrast to the case of soft wetting where solid laplace pressure was acting instead. We extended our model for that case and could provide an accurate description of the force-velocity relation of the peeling process. As in the static case, solid surface tension regularizes the crack singularity of adhesion and leads to a regular boundary condition of the soft adhesive at its contact point with the tape [Perrin et al., Soft Matter 15 (2019) 770].
Interaction Mechanisms between Sessile Droplets
Solid objects that float on the surface of a liquid are known to attract each other because they deform the surface of the liquid. This is known as the “Cheerios Effect” because it is frequently observed on milk with these cereals. But what about liquid objects (droplets) on top of a solid surface? At first sight, one would not expect any interaction because the solid merely serves as an inert support. But this interaction does exist in various scenarios that we investigate in the lab. Such interactions could be highly relevant in technological applications or in biological systems, think, for instance, of adherent cells at the surface of tissue or a biofilm.

Droplets actually pinch on solid surfaces due to capillary forces, analogous to focal adhesion of biological cells: They pull with their edge and press with their body (the net force must vanish according to Newton’s law). On glass, nothing much would happen because it is too rigid. But a soft material like a gel or a soft silicone rubber (or pudding) will deform significantly. That deformation is called the “wetting ridge”. Importantly, this ridge extends quite far beyond the droplet, which can be “sensed” by other droplets nearby [Karpitschka et al., PNAS 113 (2016) 7403]. Consider two such droplets. Will they attract or repel? That depends in a very subtle way on geometry and there are at least three length scales involved: The size of the drop, the size of the wetting ridge, and the thickness of the soft material. Tersely phrased: on thin soft layers, droplets repel, on bulky elastic blocks, they attract. Importantly, the mechanism of the interaction relies only on interfacial tensions and elasticity – it should be present for any kind of object (think about cells in our body) that pinches on soft solids. As compared to the “classical” Cheerios effect, the role of solid and liquid are exchanged, which is why we have named it the “Inverted Cheerios Effect”. But also in terms of the involved physics, it is quite different: A body force like gravitation is not required, it is a pure result of capillarity and elasticity. The resulting droplet motion is then governed by dissipation in the soft substrate, which can quantitatively be calculated and matches the observed droplet velocities well [Pandey et al., Soft Matter 13 (2017) 6000].

But is elasticity even necessary for such an effect? Couldn’t a thin liquid film on top of a rigid surface mediate a similar kind of interaction? Such scenario has recently gained great attention under the catchphrase “SLIPS”: these “Slippery Liquid-Infused Porous Surfaces” can almost fully suppress droplet pinning, and are believed to be useful in numerous technical applications. Droplets on top of such surfaces create a liquid meniscus in the film around them, very similar to the wetting ridge observed on soft surfaces [Tress et al., Soft Matter 13 (2017) 3760]. Micron-sized drops interact by a capillary mechanism when deposited on films of immiscible viscous liquids [Hack et al., Appl. Phys. Lett. 113 (2018) 183701]. This scenario is highly relevant in modern ink-jet printing, where the print substrate is typically coated with a primer liquid, e.g. to promote precipitation of color pigments. Each deposited droplet emits a capillary wave and, at the same time, interacts with the waves that are emitted by its neighbors. Consequentially, the interaction forces not only depend on geometry, but also on time. Waves are composed of a sequence of hills and valleys, for which reason the droplet interaction follows a complicated pattern of attractive and repulsive zones that in addition change over time. Despite such complicated behavior, there is an elegant description of these spatio-temporal interaction patterns. The capillary wave emitted by a droplet grows in a self-similar way. Thus the wave profiles is ‘stretched’ as time proceeds, with a power law ~t1/4, to be precise. The same scaling is recovered in the interaction pattern, and zones of repulsion and attraction are aligned with the sign of the curvature (upward or downward) of the wave profile emitted by a single droplet.












