The path to self-trapping of Bose-Einstein-condensates
Bose-Einstein condensates (BECs) trapped in periodic optical potentials have proven to be an invaluable tool to study fundamental and applied aspects of quantum optics, quantum computing and solid state physics. In the limit of large atom numbers per well, the dynamics can be well described by a mean-field approximation which leads to a lattice version of the Gross-Pitaevskii equation, the discrete nonlinear Schrödinger equation (DNLS). One of the most intriguing features of the dynamics of such nonlinear lattices is that excitations can spontaneously and stably localize even for repulsive nonlinearities. This phenomenon of discrete self-trapping, also referred to as the formation of discrete breathers or intrinsic localized modes, is a milestone discovery in nonlinear science that has sparked many studies. Discrete breathers have been observed experimentally in various physical systems such as arrays of nonlinear waveguides and Josephson junctions, spins in antiferromagnetic solids, and BECs in optical lattices.
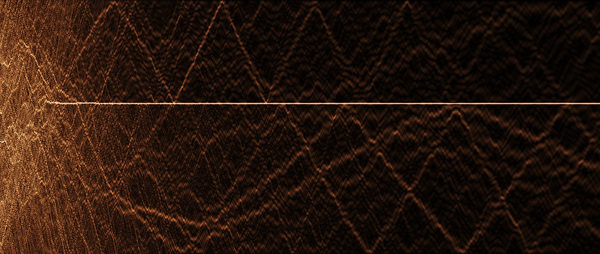
Many experiments do not allow the detailed control of the initial condition necessary to directly excite the self-trapped solutions, and more generally we need to understand the interplay of self-trapping with extended complex dynamics. It is thus an important question, how self trapped and long term stable states can get excited by general initial conditions. This fundamental question, however, had remained mostly unanswered. We have recently made progress in understanding two important mechanisms of self-trapping in BECs, that also carry over more generally to the other systems described by the DNLS. One mechanism, that leads to a very complex self-trapping scenario, is self-localization, where homogeneously extended or thermalized initial conditions can excite self trapped states in the presence of local dissipation (e.g. boundary dissipation). An example is shown in Figure above. We were able to derive an explicit prediction of the nonlinearity strength self-localization transition as a function of the system size [1,3], explaining earlier numerical work [4], and we have shown that self-localization persists beyond the mean field approximation [3].
Another approach to create self-trapped states is to study how generic localized wave packets can excite self-trapping. In a seminal work from 2001 Trombettoni and Semerzi developed a variational approach to study the mean field dynamics of Gaussian wave packets of BECs in optical lattices which has become a standard reference in the field. However, numerical simulations show strong deviations from the variational dynamics. We have therefore numerically calculated a detailed dynamical phase diagram that separates self-trapping from the diffusive and a solitonic regime by defining suitable order parameters and we were able to derive an explicit analytic expression for the self-trapping transition making use of the concept of the Peirls-Nabarro energy barrier [2].